|
A post by Roman Zhuravel and Guy Koplovitz We investigated the Erdos–Renyi model by simulating random non-directional graphs and counting (and visualizing) the number of graphs connected-components. This model describes the behavior of components' number and size in a graph G(n, p), when n→inf. The graph is constructed by connecting nodes randomly, i.e. Each edge is included in the graph with probability p, independent of every other edge. The behavior of random graphs is often studied in the case where n, the number of vertices, tends to infinity. Although p can be fixed in this case, it may also be defined as a function which depends on n. For example, the statement:
In a 1959 paper[1], Erdos and Renyi described the behavior of G(n,p) very precisely for various values of p. Their results included:
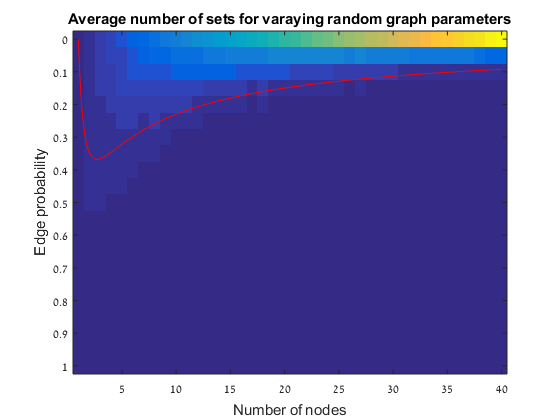
In this exercise we simulate random graphs to check the last conclusion from the paper of Erdos and Renyi: the p = ln(n)/n threshold theorem. The simulation is done as follow:
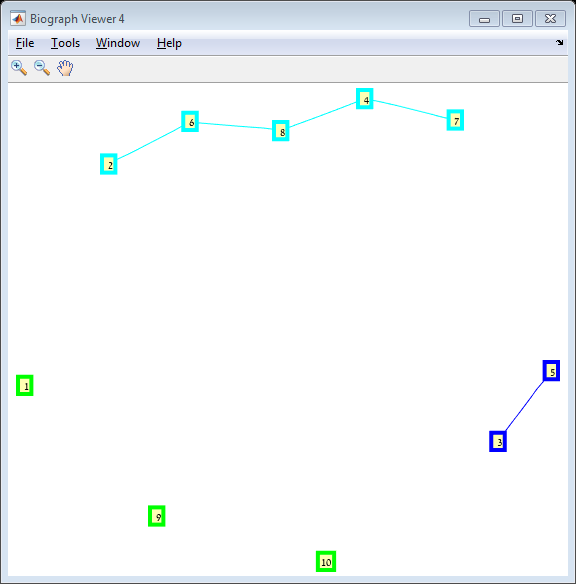
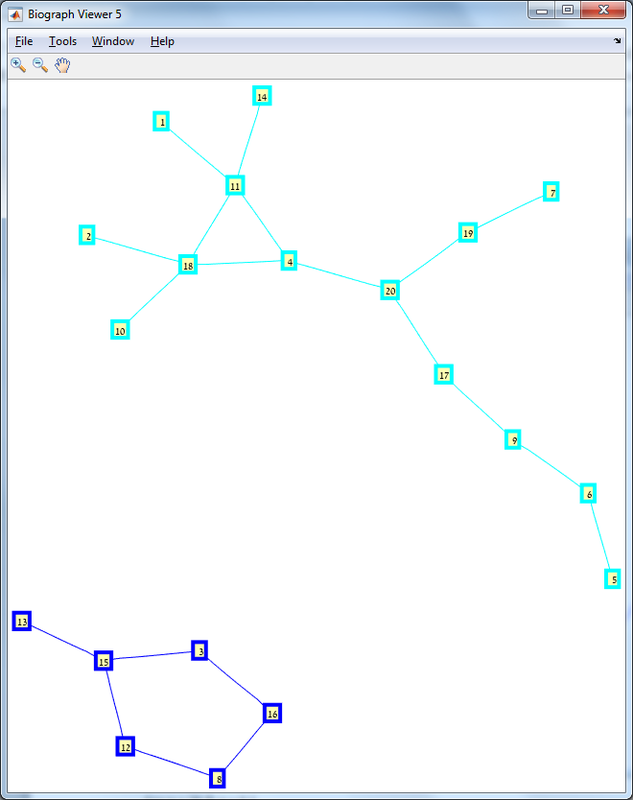
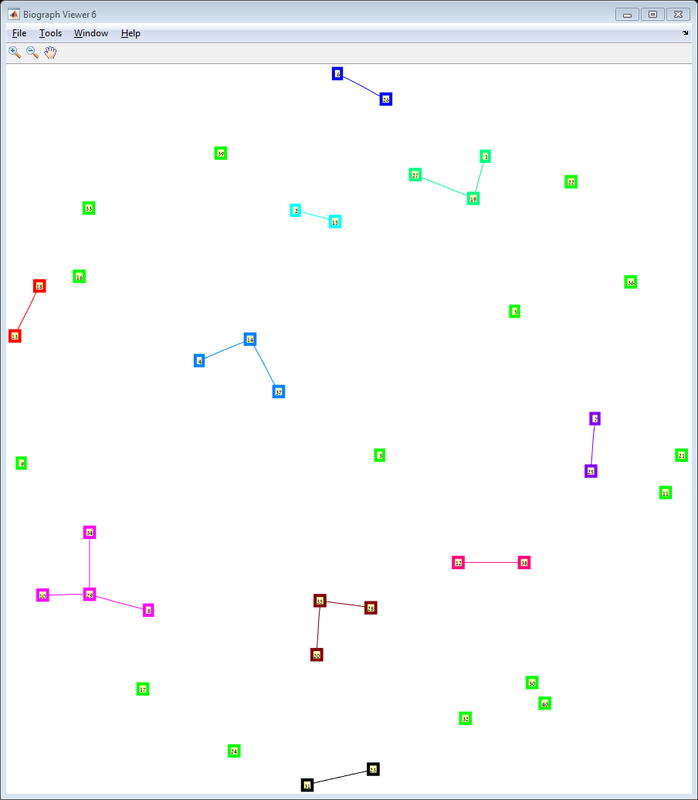
Results The red line is the p = ln(n)/n threshold which shows that the simulation follows the theory quite nicely. Representative random graphs Since those graphs are random, they might diverge from the averaging map above. For n = 10 & p = 0.15 : For n = 20 & p = 0.1: For n = 40 & p = 0.02: Methods For this exercise we used the biograph object which is a part of Matlab's Bioinformatics Toolbox.
In order to expedite long calculations we applied Matla's parallel computing capabilities. [1] - ERDdS, P., and A. R&WI. "On random graphs I." Publ. Math. Debrecen 6 (1959): 290-297. |
 RSS Feed
RSS Feed
