|
Any color may be created by a mixture of 3 colors: Red, Green and Blue [R, G, B]. If we think of a space where each axis represent the concentration of a the [R, G, B] colors (0=not at all, 1=as green as it gets), each point in this color cube represents a unique color. Without any particular reason I became interested in the following probabilistic question: I throw a fair die (i.e. draw, with replacement from a uniform distribution of the numbers {1..6}) and sum the number it shows. For example – the first throw shows 5 (the sum so far is 5), the second is 3 (the sum so far is 8), the third is 4 (the sum so far is 12) and so on. If I repeat this process, what is the chance that my sum will hit exactly 100? One could think of multiple methods to approach this problem (and here are some ideas of other smart fellows who became interested in this problem), but one approach is to simply do it – generate a large number of die tosses sequences, and count these sequences which hit exactly 100. The straightforward programmatic solution looks something like this: (And just for those of you curious - yields the result 0.298 which is very close to 2/7 which equals to 1/[the die expectation=3.5]): hit_100_counter = 0; ITERATIONS = 10000; for ii = 1:ITERATIONS die_sum = 0; while die_sum < 100 die_sum = die_sum + randi(6); end if die_sum==100 hit_100_counter = hit_100_counter + 1; end end proportion_of_100_hits = hit_100_counter/ITERATIONS This might be interesting on its own, but I became interested in this solution when presenting in class the subject of vectorization. The first lesson in every Matlab guide-book is that Matlab prefers vector operations over loops. This preference is justified by several motivations:
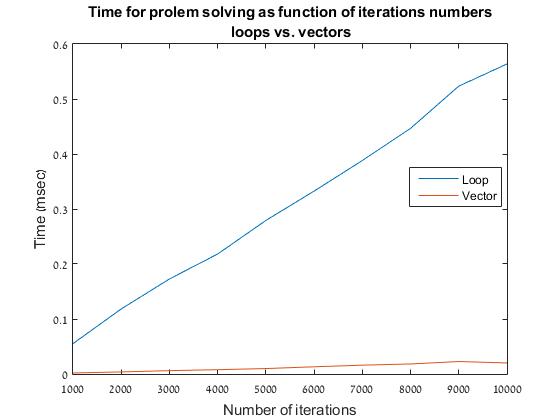
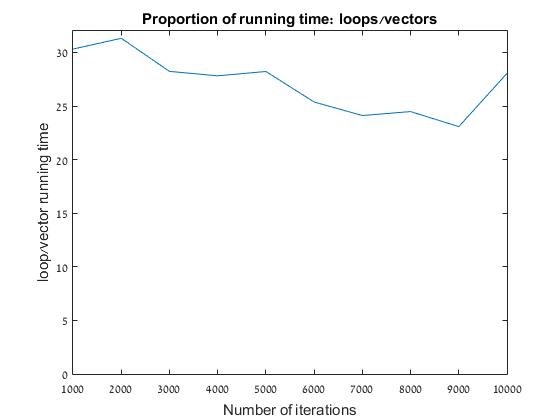
In addition to these, it is often argued that vector operation have better performances when compared to loops. I thought the “hit exactly 100” is a great opportunity to check this claim. In order to do so, the first thing to do is to vectorize the loop above. Believe it or not, but this short line replaces all the code above: mean(any(cumsum(randi(6, 100, iterations)) == 100)) We first draw 100 numbers from the [1..6] range (randi(6, 100,k))and do so k independent times (randi(6, 100,k)). We perform cumulative sum on each of the k sequences (cumsum). We count all sequences for which any of the summed elements equals 100, and the calculate the mean. This is all nice and well, but does the vectorized form actually works faster? To check this, we may try solving the problem for different numbers of iterations (for different number of independent sums of die tosses) and measure the computation time for each of the methods. Here are the results (find full code here): It turns out that indeed, vectorized code is much more efficient. Arguably, this one liner is not the most readable code, but hey - it does runs 30 times faster (so the running time saved could be invested in writing an explanatory comment :)
This simple particle animation is just fascinating to watch (code). The simulation defines 2 populations with a shared center. In the first half of the simulation, one of the populations (the multicolored one) is pulled outward from the center in random directions. In the second half of the simulation the multicolored population is drawn back to the center while the other (light blue) population expands out.
|
 RSS Feed
RSS Feed
